목차
Perceptron
- Multi-Layer-Perceptron(MLP)
- Activation Function을 가진 새로운 neuron model - [활성화 함수]
- Softmax Function - [소프트 맥스]
- Cost Function - [손실 함수]
- Gradient Descent Algorithm - [경사 하강법]
- Backpropargation - [오류-역전파]
1. Perceptron
Perceptron은 rosenblatt가 고안한 Artificial Neural Network의 기본 모델입니다.
인공지능의 초기연구는 Perceptron으로 시작하였으며, 이를 이용해서 여러 조건에 대한 가중치를 조절해서 특정 결과를 출력할 수 있습니다.
- 임의의 가중치의 값 와 를 정합니다.
- 입력 에 대해서 가중치 에 대해서 Inner Product(내적, 행렬곱, 곱)을 합니다.
matrix transpose(T) : - 그 결과를 모두 Sum(Summation, 합)을 해줍니다.
가 보다 크다면, 출력값을 1로, 그렇지 않다면 출력값을 0으로 합니다.
1-1. XOR Problem
1-1-1). AND Gate
Perceptron을 이용하면, AND Gate를 다음과 같이 구현할 수 있습니다
Gate의 입력은 0과 1로만 구성됩니다.
가중치(Weights)와, 임계값(Threshold)을 다음과 같이 설정합니다.
입력값을 Perceptron 출력값을 구하기 위한 수식에 대입해서 결과를 확인합니다.
0
0
0.5
0.5
0+0
0.4
0
1
0
0.5
0.5
0.5+0
0.4
0
0
1
0.5
0.5
0.5+0
0.4
0
1
1
0.5
0.5
0.5+0.5
0.4
1
이를 기하학적으로 표현하면 다음과 같습니다.
1-1-2). XOR Gate
Perceptron으로 XOR Gate를 구현하려고하면, 불가능합니다. 이를 쉽게 설명하기 위해, XOR Gate를 기하학적으로 표현하면 다음과 같습니다.
아래에서 보듯이, 단순한 선형 방정식으로는 XOR Gate의 출력값 분류가 불가능합니다.
2. Multi-layer Perceptron
Perceptron에서 XOR Problem의 문제처럼, Perceptron이 갖는 선형이진분류가 갖는 한계점을 돌파하기 위해 Perceptron을 여러개 쌓는 방법이 나오게 되었습니다.
이것을 Multi-Layer Perceptron이라고 합니다.
이미 우리는 NAND Gate와 AND Gate, OR Gate의 조합으로 XOR Gate를 구현할 수 있다는 사실을 알고있습니다. XOR Problem을 해결하기 위해, 이러한 고전적인 방법을 사용합니다.
Single Perceptron으로 NAND, AND, OR Gate를 만든 후, 해당 input과 Output을 연결해주는 것을 통해서 우리는 XOR Gate를 구현할 수 있습니다.
2-1) Multi-layer Perceptron의 Forward 연산
Perceptron에서 입력값과 가중치의 곱과 합으로 표현될 수 있음을 확인하였습니다.
Multi-layer Perceptron에서도 마찬가지로 모든 Forward 과정을 행렬의 곱셈으로 표현할 수 있습니다.
아래의 그림을 이용하여 설명하겠습니다.
- 여기서 상수 1은 bias를 뜻합니다. Weights값으로 수렴이 잘 안될 때, 해당 네트워크의 고계도 함수를 shift(이동)하는데 사용됩니다.
(만약 이해가 안되신다면, 해당 내용을 이해하는데 있어서 방해가 되는 내용이 아니므로 그냥 그렇구나라고 넘어가시면 되겠습니다. :: 추후 설명 예정) - 왼쪽끝을 입력(Input)이라고 하고, 첫번째 레이어의 최상단 노드에 대한 출력값을 계산한다고 생각해봅시다.
첫번째 레이어의 두번째 노드에 대한 출력값을 계산한다고 생각해봅시다.
- 첫번째 레이어의 세번째 노드에 대한 출력값을 계산한다고 생각해봅시다.
우리는 이를 다음과 같은 행렬의 곱셉으로 표현할 수 있습니다.
위와 같은 방식으로 우리는 모든 Layer의 연산을 행렬 곱으로 표현할 수 있습니다.
3. Activation function
Nueral Network에서 Activation Function이란, 출력값 y를 다음 레이어로 보내는 함수를 의미합니다.
Perceptron에서는 Activation Function을 다음 그림과 같이 Step Function(계단함수)을 사용했습니다.
Step Function과 같은 이러한 불연속함수는 미분이 안되므로, 역전파를 이용한 학습이 안되는 단점이 존재합니다.
따라서 학습을 위해, 출력값 y가 [0,1]로 맵핑되는 sigmoid함수를 주로 사용하게됩니다.
Activation function : 왼쪽이 step function, 오른쪽이 sigmoid function.
4. Softmax function
우리는 Network에서 나온 최종값이 어떠한 정답을 나타내길 원합니다. 만약 네트워크의 종단점이 Activation function으로만 끝나있다면, 우리가 확인할 수 있는 수치는
[0,1]의 값을 갖는 Activation function을 통화한 여러 숫자들뿐일 것입니다. 이를 One of K coding, 즉 output node에서 Classification을 하고자 할 때, 출력값을 모두 합치면
1이 되고, 각각의 확률을 구할 수 있는 형태로 출력값을 내고자 할 때, 사용합니다.
5. Cost function
- 속도가 선형적으로 빨라지는 빨라지는 자동차가 있다고 가정합니다.
- 해당 자동차에는 가속도 센서가 있어서, 해당 속도를 주기적으로 받아옵니다.
- 아래 그림은 해당 센서데이터와 실제 차량의 절대 속도값을 의미합니다.
- 우리는 여기서 해당 가속도 센서 A와 B의 정밀도를 수치화해야합니다.
- 어떻게 이를 수치화할 수 있을까요?
- 이러한 형태의 문제에 우리는 MSE : Mean Square Error를 사용할 수 있습니다.
- 임의의 점 (x,y)와 해당 직선 Y = ax + c의 최단거리 d를 구합니다.
- 모든 점에 대한 최단거리 d를 더합니다.
- 측정된 모든 데이터에 대한 최단거리 d의 크기가 상대적인 지표가 됩니다.
- 이러한 최단거리 d의 합을 구하는 방식을 MSE라고합니다.
6. Gradient Descent Algorithm
6-1). Differentiation
- 미분은 "변화율"을 의미합니다. 변화율은 기하학적으로 기울기를 의미합니다.
- 위의 그림에서 점 A와 점 B의 변화율(기울기)를 구하기 위해서 y축의 변화율 / x축의 변화률 → 점 B의 높이 - 점 A의 높이 / 점 B의 x좌표 - 점A의 x좌표을 구하면 됩니다.
- 여기서 B점의 높이 - 점 A의 높이를라고 하고, 점 B의 x좌표 - 점 A의 x좌표를 라고 합니다.
- 는 로 표현될 수 있습니다.
- 여기서 가 0으로 수렴한다면(0은 아니지만 0에 가까운 실수) 어느 특정 x좌표에서의 변화률을 구할 수 있게 됩니다.
- 이 특정 x좌표에서의 변화율을 미분이라고 합니다.
- 이러한 미분값을 우리는 수치해석적으로 구할 수 있습니다.
- 다음을 가정해 봅시다.
함수 y는 다음과 같고, 이미 해당 함수의 미분값은 잘 알려진 2x입니다. 만약에 x=3을 가정한다면, 우리는 x좌표 3에서의 미분값은 6임을 알 수있습니다.
이를 수치해석적으로 표현하면 다음과 같습니다. 여기서 우리는 가 0으로 수렴하는 것을 부동소수 0.005로 대체할 수 있습니다.
6-2). Partial Differentiation
우리는 위의 1차 미분을 3차원 공간에서의 2차 미분(편미분)으로 확장할 수 있습니다.
편미분이란 2차원 이상의 고계함수에서 어떤 특정 방향의 미분값을 의미합니다.
- 해당 z함수는 아래 왼쪽 그림과 같은 곡면함수를 의미합니다.
- 우리는 해당 곡면함수에서 x방향의 미분값과 y방향의 미분값을 구할 수 있습니다.
- 이러한 x방향의 미분값, y방향의 미분값을 구하는 것을 편미분이라고 합니다.
- 이러한 편미분도 1차 미분과 같이 수치해석적으로 구할 수 있으며, 이를 확장하면 360도 방향의 모든 편미분값을 구할수있습니다.
6-3). Gradient Descent Algorithm
- Gradient Descent Algorithm은 아래 그림과 같이 수식으로 표현될 수 있습니다.
은 다음(next, 미래의) x 값을 의미합니다. 은 현재의 x값을 의미합니다. (감마)는 learning rate(학습률)을 의미합니다.
은 현재 x값에 대한 함수F의 미분값을 의미합니다.
- 따라서 Gradient Descent Algorithm을 에서 을 가정하면 다음과 같이 적용할 수 있습니다.
- 여기서 우리는 파라미터를 다음과 같이 설정합니다.
해당 이 0에 수렴할 때까지 이를 반복합니다.
6. Backpropagation
Backpropagation은 측정된 Cost를 기점으로 에러를 역전파하여 가중치 Weights와 bias의 값을 조정하는 알고리즘입니다.
Backpropagation의 이해를 위해서 Artificial Neural Network의 학습 프로세스를 다시 한번 살펴보면 아래와 같습니다.
Infinite loop until Cost Minimized
- Feed Forward
- Error measurement
- Backpropagation (Update parameter)
Backpropagation을 간단한 예제로 확인해보면 다음과 같습니다.
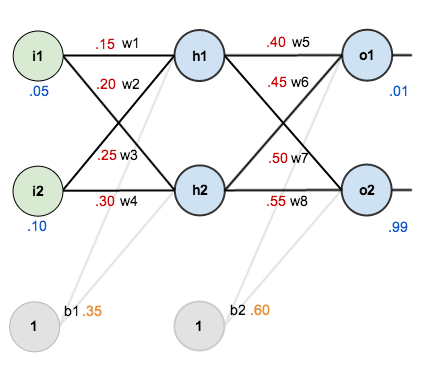
우리는 2개의 input node를 가지고 2개의 output node, 2개의 bias를 갖으며, 2개의 layer를 가진 multi-layer perceptron을 가정합니다.
해당 multi-layer perceptron은 다음과 같습니다.
여기서 우리는 각각의 input과 weights의 값, 그리고 기대하는 output의 값(labeling)을 결정합니다.
이제 이를 통해서 Artificial Neural Network의 trainning processing의 one iteration을 진행해보겠습니다.
Forward Pass
- 1 layer의 첫번째 노드 출력값을 구합니다.
- 1 layer의 첫번째 노드의 최종 출력값을 구하기 위해, Activation function에 노드 출력값 입력합니다.
* 해당 예제의 Activation function은 sigmoid를 사용하였습니다. - 이런형태로 1 layer의 두번째 노드의 최종출력값을 구하면 다음과 같습니다.
- 이렇게 네트워크 종단에 있는 첫번째 출력노드의 출력값을 구하면 다음과 같습니다.
- 네트워크 종단의 두번째 출력노드의 출력값은 다음과 같습니다.
Cost Mesurement
- 최종 출력값을 얻었으니, 이제 기대했던 출력값과 현재 네트워크의 출력차이(에러)를 측정합니다.
Backpropagation
- 최종 출력값을 얻었으니, 이를 통해서 parameter updating을 해줄 차례입니다.
- 여기서 우리는 각각의 weights들이 얼마나 현재 Error에 기여했는지 알아야합니다.
이를 위해서, 우리는 Error를 최소화하는 방향으로 parameter update를 할 수 있습니다.
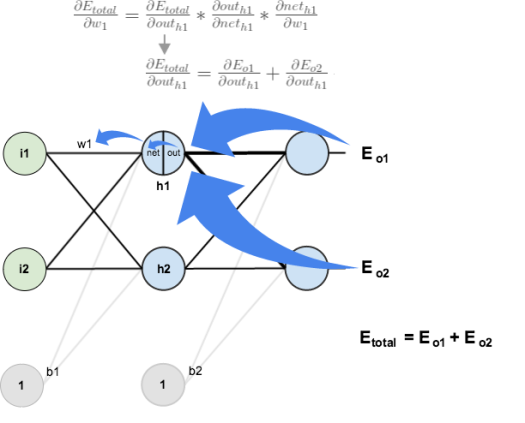
여기서 우리는 chain rule을 사용할 것입니다. chain rule은 다음과 같습니다.
이를 시각화하면 다음과 같습니다. - 이제 chain rule을 구성하고 있는 요소들을 구합니다.
- 먼저 총 Error에 대한 출력 O1의 기여도를 구합니다.
- 이제 출력 O1에 대한 net_o1에 대한 기여도를 구합니다.
- 마지막으로 net_o1에 대한 w5의 기여도를 구합니다.
- 이제 이 셋을 모두 합칩니다.
- Backpropagation에서 이러한 chain rule을 delta rule이라고 합니다. delta rule은 다음과 같습니다.
여기서 우리는 net_o1이 전체 Error에 기여한 정도를 delta_o1이라고합니다. delta_o1은 다음과 같습니다.
여기서 delta_o1은 다음과 같이 표현될 수 있습니다.
그러므로, 전체 에러에 대한 w5의 기여도의 크기는 다음과 같이 표현될 수 있습니다.
몇몇 자료들에는 이러한 표현에 negative sign을 붙여 다음과 같이 표현하기도 합니다. - 해당 가중치가 전체 Error에 얼만큼 기여했는지 모두 구했으므로, 마지막으로 해당 가중치를 업데이트 합니다.
- 이런 형태로 가중치들을 업데이트한다면, 업데이트된 가중치들의 값은 다음과 같습니다.
- 이렇게 같은 방식으로 더 앞에있는 레이어의 가중치들도 업데이트를 진행하면 됩니다.
7. 추가 자료
'IT > Deeplearning' 카테고리의 다른 글
| [Performance Measurement] Precision/Accuracy (2) | 2017.10.19 |
|---|---|
| [번역:: Gradient Clipping] Why you should use gradient clipping (0) | 2017.10.15 |
| [CNN] Convolution Neural Network (0) | 2017.10.15 |
| [Material] 비숍의 패턴인식과 머신러닝 (0) | 2017.10.13 |
| [YOLO DARKNET] 구성 및 설치, 사용방법 (0) | 2017.06.04 |